| Pos. | Giocatore | Punti |
|---|
| Pos. | Giocatore | Punti |
|---|
| Pos. | Giocatore | Punti |
|---|

BUL GAME è un gioco online utile per consolidare le conoscenze dei valori di verità e falsità e dei connettivi logici. Il gioco si svolge premendo opportunamente i pulsanti A e B - da tastiera oppure con il mouse - secondo le indicazioni che vengono fornite. Se si preme il pulsante giusto si fa 1 punto, se si sbaglia la partita finisce. L'obiettivo è realizzare più punti possibile. Occorre prestare attenzione perché le indicazioni vengono fornite alcune volte dai cavalieri, personaggi affidabili che dicono sempre la verità, e altre dai furfanti, personaggi non affidabili che mentono sempre.
Nella pagina iniziale si sceglie come impostare la partita.

-
TIPO DI DOMANDA
Si sceglie la struttura logica delle questioni che vengono poste, si può selezionare anche più di un’alternativa.

In questo primo tipo di esercizi bisogna riconoscere affermazioni vere e false, facendo cioè attenzione al personaggio che le pronuncia. Precisiamo che ad ogni turno è necessario premere A o B per continuare (se non si preme niente non si passa al turno successivo).
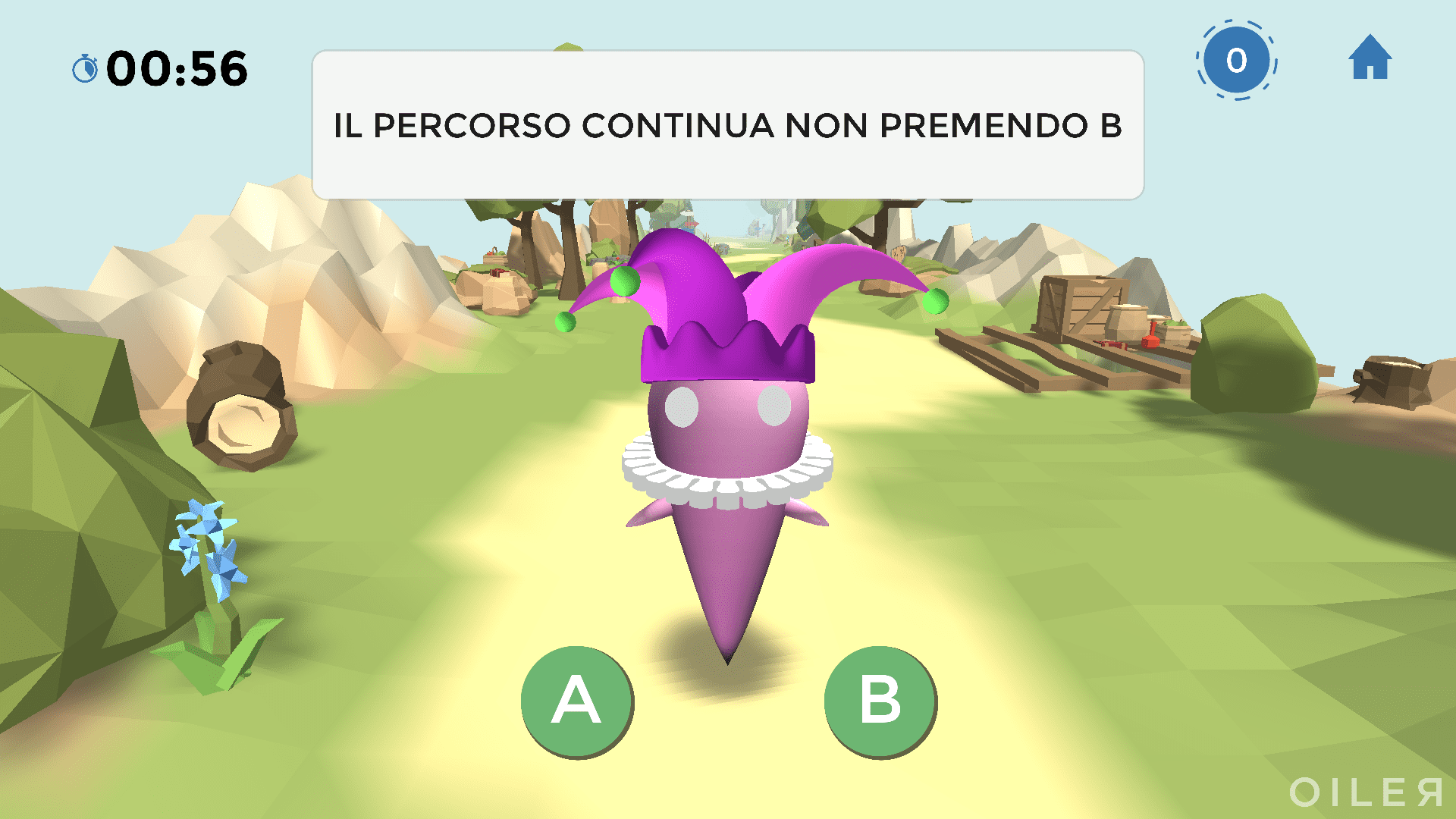
Nell’esempio in figura, il furfante suggerisce di non premere B: la risposta giusta è proprio quella di premere B, poiché il furfante mente sempre.

Nella sezione predicati compaiono scritture del tipo ANIMALE (TIGRE): questa scrittura va letta come “la tigre è un animale”. In generale X(Y) va letto come “Y è del tipo X”.

Nell’esempio in figura, poiché Londra è effettivamente una città e parla un cavaliere, la risposta giusta è la A.

La sezione negazione introduce il simbolo NOT;
¬ ANIMALE (TIGRE) va letto come “la tigre NON è un animale”. In generale ¬ X(Y) va letto come “Y non è del tipo X”.
Nell’esempio in figura compare la scritta ¬ COLORE (ROSA), che va letta come “il rosa non è un colore”. Poiché il rosa è in realtà un colore e a parlare è un cavaliere, la risposta giusta è la A.

Nella sezione viene introdotto il simbolo AND;
A ∧ B è vero se sia A sia B sono veri. Per esempio ANIMALE (TIGRE) ∧ ANIMALE (ORSO) è vero, ma ANIMALE (TIGRE) ∧ ANIMALE (SEDIA) è falso.
Nell’esempio in figura compare la scritta FRUTTO (PERA) ∧ FRUTTO (MELO), che è falsa perché il melo non è un frutto (ma un albero da frutta!). La risposta giusta è quindi B perché a parlare è un furfante.

Nella sezione viene introdotto il simbolo OR;
A ∨ B è vero se almeno uno fra A e B è vero. Per esempio ANIMALE (TIGRE) ∨ ANIMALE (SEDIA) è vero, mentre ANIMALE (SEDIA) ∨ ANIMALE (TAVOLO) è falso.

Nella sezione viene introdotto il simbolo ESCLUSIONE;
A \ B è vero solamente nel caso in cui A è vero e B è falso. Per esempio ANIMALE (TIGRE) \ ANIMALE (SEDIA) è vero.

Nella sezione viene introdotta l'implicazione;
A → B è vero in tre casi differenti: se A e B sono entrambi veri, se sono entrambi falsi, e se A è falso e B è vero. Per esempio ANIMALE (TIGRE) → ANIMALE (SEDIA) è falso, mentre sia ANIMALE (TIGRE) → ANIMALE (ORSO), sia ANIMALE (TAVOLO) → ANIMALE (SEDIA), sia ANIMALE (TAVOLO) → ANIMALE (ORSO) sono veri.
-
TIPOLOGIA PREDICATI
Si sceglie la tipologia dei predicati, cioè se le affermazioni che vengono fatte riguardano un ambito generale di conoscenze elementari oppure specificamente la matematica. I predicati sono scritture del tipo
ANIMALE (TIGRE) dove appunto si "predica" che una certa proprietà valga su un certo soggetto.Specifichiamo ora meglio il significato di alcuni predicati matematici che compaiono nel livello 2.
MULTIPLO_3 (n) va letto come "Il numero n è multiplo di 3". Perché n sia multiplo di 3 deve esistere un numero intero k per cui n = k × 3. Per esempio 15 è multiplo di 3 perché 15 = 5 × 3, mentre 10 non è multiplo di 3 perché 10 = k × 3 non ammette soluzioni intere.
QUADRATO (n) va letto come "Il numero n è un quadrato". Perché n sia un quadrato deve esistere un numero intero k per cui n = k × k. Per esempio 16 è un quadrato perché 16 = 4 × 4, mentre 15 non è un quadrato perché 15 = k × k non ammette soluzioni intere.
-
TEMPO A DISPOSIZIONE
Si sceglie la durata massima della partita (1, 2, 4 minuti).
Se si selezionano tutte le tipologie fino alla ∧, allora la ∧, così come la ∨, verrà giocata in una nuova mappa.
Se si selezionano tutte le tipologie fino all'esclusione, allora l'esclusione, così come l'implicazione, verrà giocata in una nuova mappa.
BUL GAME è un gioco online utile per consolidare le conoscenze dei valori di verità e falsità e dei connettivi logici. Il gioco si svolge premendo opportunamente i pulsanti A e B - da tastiera oppure con il mouse - secondo le indicazioni che vengono fornite. Se si preme il pulsante giusto si fa 1 punto, se si sbaglia la partita finisce. L'obiettivo è realizzare più punti possibile. Occorre prestare attenzione perché le indicazioni vengono fornite alcune volte dai cavalieri, personaggi affidabili che dicono sempre la verità, e altre dai furfanti, personaggi non affidabili che mentono sempre.
Nella pagina iniziale si sceglie come impostare la partita.

-
TIPO DI DOMANDA
Si sceglie la struttura logica delle questioni che vengono poste, si può selezionare anche più di un’alternativa.

In questo primo tipo di esercizi bisogna riconoscere affermazioni vere e false, facendo cioè attenzione al personaggio che le pronuncia. Precisiamo che ad ogni turno è necessario premere A o B per continuare (se non si preme niente non si passa al turno successivo).

Nell’esempio in figura, il furfante suggerisce di non premere B: la risposta giusta è proprio quella di premere B, poiché il furfante mente sempre.

Nella sezione predicati compaiono scritture del tipo ANIMALE (TIGRE): questa scrittura va letta come “la tigre è un animale”. In generale X(Y) va letto come “Y è del tipo X”.

Nell’esempio in figura, poiché Londra è effettivamente una città e parla un cavaliere, la risposta giusta è la A.

La sezione negazione introduce il simbolo NOT;
¬ ANIMALE (TIGRE) va letto come “la tigre NON è un animale”. In generale ¬ X(Y) va letto come “Y non è del tipo X”.
Nell’esempio in figura compare la scritta ¬ COLORE (ROSA), che va letta come “il rosa non è un colore”. Poiché il rosa è in realtà un colore e a parlare è un cavaliere, la risposta giusta è la A.

Nella sezione viene introdotto il simbolo AND;
A ∧ B è vero se sia A sia B sono veri. Per esempio ANIMALE (TIGRE) ∧ ANIMALE (ORSO) è vero, ma ANIMALE (TIGRE) ∧ ANIMALE (SEDIA) è falso.
Nell’esempio in figura compare la scritta FRUTTO (PERA) ∧ FRUTTO (MELO), che è falsa perché il melo non è un frutto (ma un albero da frutta!). La risposta giusta è quindi B perché a parlare è un furfante.

Nella sezione viene introdotto il simbolo OR;
A ∨ B è vero se almeno uno fra A e B è vero. Per esempio ANIMALE (TIGRE) ∨ ANIMALE (SEDIA) è vero, mentre ANIMALE (SEDIA) ∨ ANIMALE (TAVOLO) è falso.

Nella sezione viene introdotto il simbolo ESCLUSIONE;
A \ B è vero solamente nel caso in cui A è vero e B è falso. Per esempio ANIMALE (TIGRE) \ ANIMALE (SEDIA) è vero.

Nella sezione viene introdotta l'implicazione;
A → B è vero in tre casi differenti: se A e B sono entrambi veri, se sono entrambi falsi, e se A è falso e B è vero. Per esempio ANIMALE (TIGRE) → ANIMALE (SEDIA) è falso, mentre sia ANIMALE (TIGRE) → ANIMALE (ORSO), sia ANIMALE (TAVOLO) → ANIMALE (SEDIA), sia ANIMALE (TAVOLO) → ANIMALE (ORSO) sono veri.
-
TIPOLOGIA PREDICATI
Si sceglie la tipologia dei predicati, cioè se le affermazioni che vengono fatte riguardano un ambito generale di conoscenze elementari oppure specificamente la matematica. I predicati sono scritture del tipo
ANIMALE (TIGRE) dove appunto si "predica" che una certa proprietà valga su un certo soggetto.Specifichiamo ora meglio il significato di alcuni predicati matematici che compaiono nel livello 2.
MULTIPLO_3 (n) va letto come "Il numero n è multiplo di 3". Perché n sia multiplo di 3 deve esistere un numero intero k per cui n = k × 3. Per esempio 15 è multiplo di 3 perché 15 = 5 × 3, mentre 10 non è multiplo di 3 perché 10 = k × 3 non ammette soluzioni intere.
QUADRATO (n) va letto come "Il numero n è un quadrato". Perché n sia un quadrato deve esistere un numero intero k per cui n = k × k. Per esempio 16 è un quadrato perché 16 = 4 × 4, mentre 15 non è un quadrato perché 15 = k × k non ammette soluzioni intere.
-
TEMPO A DISPOSIZIONE
Si sceglie la durata massima della partita (1, 2, 4 minuti).
Se si selezionano tutte le tipologie fino alla ∧, allora la ∧, così come la ∨, verrà giocata in una nuova mappa.
Se si selezionano tutte le tipologie fino all'esclusione, allora l'esclusione, così come l'implicazione, verrà giocata in una nuova mappa.
Bul Game a scuola
BUL GAME è un software che si presta bene per accompagnare delle attività in ambito didattico.
Quanto segue è tratto da Bernardi, L. (2022). Bul Game: Playing With Knights and Knaves. In C. A. Huertas-Abril, E. Fernández-Ahumada, & N. Adamuz-Povedano (Eds.), Handbook of Research on International Approaches and Practices for Gamifying Mathematics (pp. 170–188). IGI Global.
Prima di approfondire il discorso sulla correttezza del gioco, cominciamo con una precisazione: quando, per esempio, il cavaliere dice "Il percorso continua non premendo A", a priori anche il non premere alcun tasto è un'azione corretta. Nel gioco c'è quindi il tacito accordo che sia obbligatorio ad ogni turno premere A oppure B (i.e. A aut B).
Il discorso più tecnico riguarda invece le frasi in cui compare un'altra condizione, cioè del tipo "if X then Y else Z". Per quanto detto prima, Z è sempre del tipo ¬Y. Questo fa sì che dire "if X then Y else Z" equivalga a dire "X iff Y", i.e. X ↔ Y. Sia ora K una variabile per personaggi (più precisamente, K indica che chi parla è un cavaliere) e sia P una qualsiasi affermazione. Se un personaggio afferma P è sempre verificato K ↔ P. In particolare, nel gioco, P = X ↔ Y. Abbiamo quindi che ogni turno del gioco può essere riscritto come K ↔ (X ↔ Y). Quindi se K non è verificata, i.e. chi parla è un furfante, allora anche X ↔ Y deve essere falsa, cioè i valori di verità di X e Y devono essere diversi. Se invece chi parla è un cavaliere, K è verificato e quindi i valori di verità di X e Y devono coincidere. Per approfondire il discorso e tendere ai teoremi di Godel, consigliamo la lettura del libro Forever Undecided di Raymond Smyullyan (Knopf, 1987).